1. Executive Summary
The Golden Chain blockchain represents a significant advancement in decentralized ledger technology, addressing the longstanding blockchain trilemma of security, scalability, and decentralization. Utilizing a robust Proof-of-Stake (PoS) consensus mechanism, Golden Chain ensures unparalleled security while maintaining high transaction throughput and broad decentralization. The native token, $GCHAIN, facilitates seamless transactions, staking, and governance, empowering a community-driven ecosystem.
2. Introduction
2.1. Background
Blockchain technology has revolutionized the way decentralized systems operate, offering transparency, security, and immutability. However, achieving an optimal balance between security, scalability, and decentralization—commonly referred to as the blockchain trilemma—has been a persistent challenge.
2.2. Objectives
The primary objective of the Golden Chain project is to develop a blockchain that simultaneously excels in security, scalability, and decentralization. By leveraging innovative consensus mechanisms and optimized network protocols, Golden Chain aims to set a new standard in blockchain performance and reliability.
3. Blockchain Fundamentals
3.1. What is Blockchain?
A blockchain is a distributed ledger technology that records transactions across a network of computers. Each block contains a list of transactions, and blocks are linked using cryptographic hashes, ensuring the integrity and immutability of the data.
3.2. Consensus Mechanisms
Consensus mechanisms are protocols that ensure all nodes in a blockchain network agree on the state of the ledger. Common mechanisms include Proof-of-Work (PoW), Proof-of-Stake (PoS), and Delegated Proof-of-Stake (DPoS).
4. Golden Chain Overview
4.1. Vision and Mission
Golden Chain aspires to create a decentralized ecosystem that empowers users by providing a secure, scalable, and highly decentralized blockchain platform. Our mission is to overcome the limitations of existing blockchains and foster widespread adoption through technological excellence and community engagement.
4.2. Key Features
- Proof-of-Stake Consensus: Ensures energy efficiency and security.
- High Throughput: Capable of processing thousands of transactions per second.
- Decentralized Governance: Community-driven decision-making processes.
- Interoperability: Seamless integration with other blockchain networks and traditional systems.
5. $GCHAIN Token
5.1. Tokenomics
The $GCHAIN token serves as the native currency of the Golden Chain ecosystem. It is used for transaction fees, staking, governance voting, and incentivizing network participants.
- Total Supply: 1,000,000,000 $GCHAIN
- Distribution:
- 50% Staking Rewards
- 20% Development Fund
- 15% Community and Marketing
- 10% Reserve
- 5% Team and Advisors
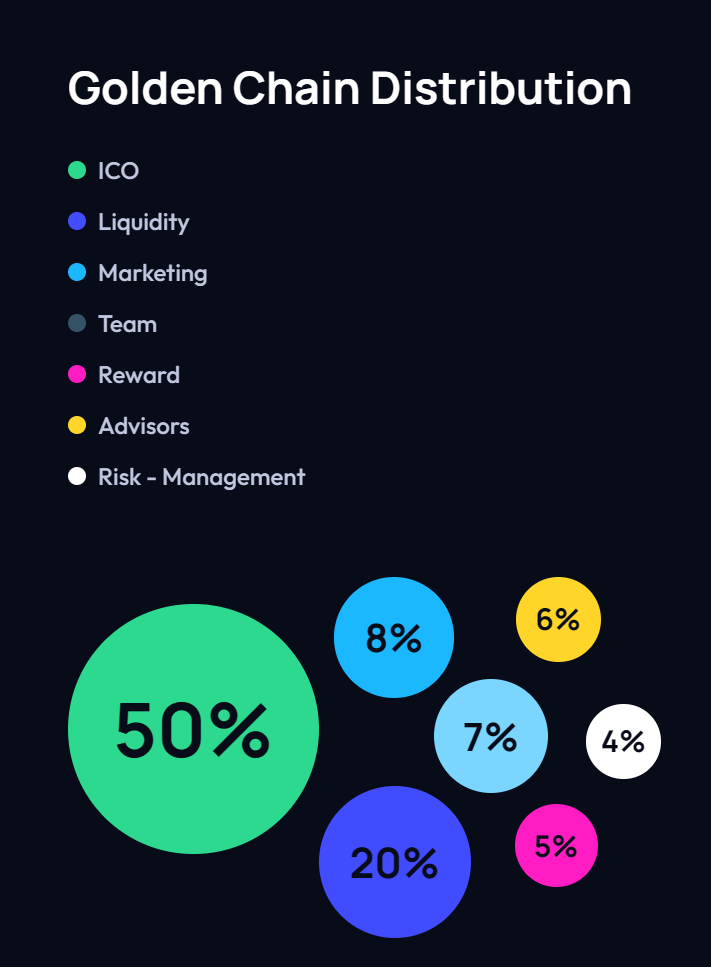
Figure 1: $GCHAIN Token Distribution
5.2. Use Cases
- Transaction Fees: Facilitating smooth and cost-effective transactions.
- Staking: Securing the network and earning rewards.
- Governance: Participating in protocol upgrades and decision-making.
- Incentives: Rewarding developers and contributors for their efforts.
6. Proof-of-Stake Consensus Mechanism
6.1. Mechanism Details
Golden Chain utilizes an advanced Proof-of-Stake (PoS) consensus mechanism designed to enhance security, efficiency, and decentralization. Unlike Proof-of-Work (PoW), which relies on computational power, PoS selects validators based on the number of tokens they hold and are willing to "stake" as collateral.
6.1.1. Validator Selection Algorithm
The validator selection process in Golden Chain is governed by the following algorithm:
Stake Weight Calculation
Each validator's weight \( W_i \) is determined by the amount of $GCHAIN tokens staked \( S_i \) and the staking duration \( D_i \).
\[ W_i = S_i \times \left(1 + \frac{D_i}{T}\right) \]
Where:
- \( W_i \) = Weight of validator \( i \)
- \( S_i \) = Staked tokens by validator \( i \)
- \( D_i \) = Duration of staking for validator \( i \)
- \( T \) = Maximum staking duration threshold
Randomized Selection
Validators are selected probabilistically based on their weight. The probability \( P_i \) of selecting validator \( i \) is:
\[ P_i = \frac{W_i}{\sum_{j=1}^{N} W_j} \]
Where:
- \( N \) = Total number of validators
- \( W_j \) = Weight of validator \( j \)
Committee Formation
A committee of \( K \) validators is formed for each epoch to propose and validate blocks.
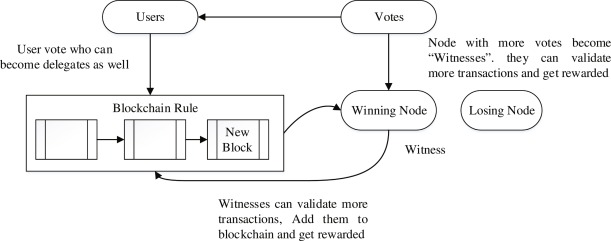
Figure 2: Consensus Committee Formation Process
6.1.2. Epoch Structure
The blockchain operates in epochs, each comprising multiple blocks. The epoch structure ensures regular validator rotation and system updates.
- Epoch Duration (\( E \)): Defined in blocks (e.g., 100 blocks per epoch).
- Block Time (\( B \)): Time between blocks (e.g., 10 seconds).
The total time per epoch is:
\[ \text{Total Epoch Time} = E \times B \]
10. Economic Model
10.2. Staking Rewards
10.2.1. Reward Calculation Formula
The staking reward \( R \) for a validator is determined by:
\[ R = \frac{A \times P \times (1 - F)}{T} \]
Where:
- \( R \) = Reward
- \( A \) = Annual staking rewards pool
- \( P \) = Proportion of stake
- \( F \) = Fee percentage
- \( T \) = Total staked tokens
10.2.2. Example Calculation
Assume:
- \( A = 10,000,000 \) $GCHAIN
- \( P = \frac{S_i}{T} = \frac{1,000,000}{100,000,000} = 0.01 \)
- \( F = 0.05 \) (5% fee)
- \( T = 100,000,000 \) $GCHAIN
\[ R = \frac{10,000,000 \times 0.01 \times (1 - 0.05)}{100,000,000} = \frac{95,000}{100,000,000} = 0.00095 \text{ $GCHAIN per token staked annually} \]
10.2.3. Projected Staking Rewards Over Time
Figure 3: Projected Staking Rewards Over Time
11. Smart Contracts and dApps
11.1. Smart Contract Functionality
Golden Chain supports Turing-complete smart contracts, enabling the creation of decentralized applications (dApps) across various industries, including finance, supply chain, and gaming.
11.1.1. Example Smart Contract in Solidity
// SPDX-License-Identifier: MIT
pragma solidity ^0.8.0;
contract GChainToken {
string public name = "Golden Chain Token";
string public symbol = "GCHAIN";
uint8 public decimals = 18;
uint256 public totalSupply;
mapping(address => uint256) public balanceOf;
mapping(address => mapping(address => uint256)) public allowance;
event Transfer(address indexed from, address indexed to, uint256 value);
event Approval(address indexed owner, address indexed spender, uint256 value);
constructor(uint256 initialSupply) {
totalSupply = initialSupply * (10 ** uint256(decimals));
balanceOf[msg.sender] = totalSupply;
emit Transfer(address(0), msg.sender, totalSupply);
}
function transfer(address _to, uint256 _value) public returns (bool success){
require(balanceOf[msg.sender] >= _value, "Insufficient balance.");
balanceOf[msg.sender] -= _value;
balanceOf[_to] += _value;
emit Transfer(msg.sender, _to, _value);
return true;
}
function approve(address _spender, uint256 _value) public returns (bool success){
allowance[msg.sender][_spender] = _value;
emit Approval(msg.sender, _spender, _value);
return true;
}
function transferFrom(address _from, address _to, uint256 _value) public returns (bool success){
require(_value <= balanceOf[_from], "Insufficient balance.");
require(_value <= allowance[_from][msg.sender], "Allowance exceeded.");
balanceOf[_from] -= _value;
balanceOf[_to] += _value;
allowance[_from][msg.sender] -= _value;
emit Transfer(_from, _to, _value);
return true;
}
}
Explanation: This Solidity contract defines the $GCHAIN token adhering to the ERC-20 standard. It includes functionalities for transferring tokens, approving allowances, and transferring tokens on behalf of another address.
12. Solving the Blockchain Trilemma
12.1. Security
Golden Chain achieves robust security through its PoS mechanism, economic incentives, and cryptographic safeguards. The security parameter \( \lambda \) can be quantified as:
\[ \lambda = \frac{V}{C} \]
Where:
- \( V \) = Total value staked
- \( C \) = Cost to perform a 51% attack
A higher \( \lambda \) indicates stronger security.
12.2. Scalability
To address scalability, Golden Chain employs Layer 2 solutions and efficient block propagation protocols, achieving high transaction throughput without sacrificing decentralization or security.
\[ T = \sum_{s=1}^{S} T_s + T_{\text{Layer2}} \]
Where:
- \( S \) = Number of shards
- \( T_s \) = Transaction rate per shard
- \( T_{\text{Layer2}} \) = Transaction rate from Layer 2 solutions
12.3. Decentralization
Golden Chain promotes decentralization by maintaining a large and diverse set of validators. The decentralization index \( \Delta \) is calculated using the Gini Coefficient to measure inequality in stake distribution:
\[ \Delta = \frac{\sum_{i=1}^{N} \sum_{j=1}^{N} |S_i - S_j|}{2N^2 \mu} \]
Where:
- \( S_i \) = Staked tokens by validator \( i \)
- \( \mu \) = Mean staked tokens per validator
- \( N \) = Total number of validators
A lower \( \Delta \) indicates a more decentralized network.
12.4. Golden Chain's Solution
Golden Chain combines technological innovations and community-driven governance to address each aspect of the trilemma. By integrating efficient consensus mechanisms, scalable architecture, and decentralized governance, Golden Chain ensures a balanced and resilient blockchain platform.
| Trilemma Element | Golden Chain's Solution |
|---|---|
| Security | Enhanced PoS mechanism, slashing, and cryptographic protocols |
| Scalability | Sharding and Layer 2 integration |
| Decentralization | Diverse validator set and decentralized governance |
13. Advanced Mathematical Models
13.1. Incentive Optimization for Validators
To ensure optimal participation and security within the Golden Chain network, validator incentives must be meticulously balanced. We introduce an Incentive Optimization Model that maximizes validator participation while minimizing the risk of centralization.
13.1.1. Objective Function
The primary objective is to maximize the total utility \( U \) of validators, defined as the sum of staking rewards \( R_i \) and penalties \( P_i \):
\[ U = \sum_{i=1}^{N} \left( R_i - P_i \right) \]
Where:
- \( N \) = Total number of validators
- \( R_i \) = Staking rewards for validator \( i \)
- \( P_i \) = Penalties for validator \( i \) due to slashing or inactivity
13.1.2. Constraints
To maintain network security and decentralization, the following constraints are imposed:
1. Total Staked Tokens Constraint
\[ \sum_{i=1}^{N} S_i = V_{\text{total}} \]
Where:
- \( S_i \) = Staked tokens by validator \( i \)
- \( V_{\text{total}} \) = Total tokens staked in the network
2. Minimum Staking Requirement
\[ S_i \geq S_{\text{min}}, \quad \forall i \in \{1, 2, \dots, N\} \]
Where:
- \( S_{\text{min}} \) = Minimum tokens required to stake as a validator
3. Penalty Proportionality
\[ P_i = \beta \times S_i \]
Where:
- \( \beta \) = Penalty coefficient (e.g., 10%)
13.1.3. Optimization Problem
Formulating the optimization problem to maximize \( U \) subject to the constraints:
\[ \begin{aligned} \text{Maximize} \quad & U = \sum_{i=1}^{N} \left( R_i - \beta S_i \right) \\ \text{Subject to} \quad & \sum_{i=1}^{N} S_i = V_{\text{total}} \\ & S_i \geq S_{\text{min}}, \quad \forall i \in \{1, 2, \dots, N\} \end{aligned} \]
13.1.4. Lagrangian Formulation
To solve the constrained optimization problem, we employ the method of Lagrange multipliers. The Lagrangian \( \mathcal{L} \) is defined as:
\[ \mathcal{L} = \sum_{i=1}^{N} \left( R_i - \beta S_i \right) + \lambda \left( V_{\text{total}} - \sum_{i=1}^{N} S_i \right) + \sum_{i=1}^{N} \mu_i (S_i - S_{\text{min}}) \]
Where:
- \( \lambda \) = Lagrange multiplier for the total staked tokens constraint
- \( \mu_i \) = Lagrange multiplier for the minimum staking requirement of validator \( i \)
13.1.5. First-Order Conditions
Setting the partial derivatives of \( \mathcal{L} \) with respect to \( S_i \) and \( \lambda \) to zero:
\[ \frac{\partial \mathcal{L}}{\partial S_i} = -\beta - \lambda + \mu_i = 0 \quad \forall i \]
\[ \frac{\partial \mathcal{L}}{\partial \lambda} = V_{\text{total}} - \sum_{i=1}^{N} S_i = 0 \]
\[ \frac{\partial \mathcal{L}}{\partial \mu_i} = S_i - S_{\text{min}} \geq 0 \quad \forall i \]
From the first condition:
\[ \lambda = \mu_i - \beta \]
Given that \( \mu_i \geq 0 \), the optimal staking \( S_i^* \) can be derived based on whether \( S_i^* > S_{\text{min}} \) or \( S_i^* = S_{\text{min}} \).
14. Smart Contracts and dApps
14.1. Smart Contract Functionality
Golden Chain supports Turing-complete smart contracts, enabling the creation of decentralized applications (dApps) across various industries, including finance, supply chain, and gaming.
14.1.1. Example Smart Contract in Solidity
// SPDX-License-Identifier: MIT
pragma solidity ^0.8.0;
contract GChainToken {
string public name = "Golden Chain Token";
string public symbol = "GCHAIN";
uint8 public decimals = 18;
uint256 public totalSupply;
mapping(address => uint256) public balanceOf;
mapping(address => mapping(address => uint256)) public allowance;
event Transfer(address indexed from, address indexed to, uint256 value);
event Approval(address indexed owner, address indexed spender, uint256 value);
constructor(uint256 initialSupply) {
totalSupply = initialSupply * (10 ** uint256(decimals));
balanceOf[msg.sender] = totalSupply;
emit Transfer(address(0), msg.sender, totalSupply);
}
function transfer(address _to, uint256 _value) public returns (bool success){
require(balanceOf[msg.sender] >= _value, "Insufficient balance.");
balanceOf[msg.sender] -= _value;
balanceOf[_to] += _value;
emit Transfer(msg.sender, _to, _value);
return true;
}
function approve(address _spender, uint256 _value) public returns (bool success){
allowance[msg.sender][_spender] = _value;
emit Approval(msg.sender, _spender, _value);
return true;
}
function transferFrom(address _from, address _to, uint256 _value) public returns (bool success){
require(_value <= balanceOf[_from], "Insufficient balance.");
require(_value <= allowance[_from][msg.sender], "Allowance exceeded.");
balanceOf[_from] -= _value;
balanceOf[_to] += _value;
allowance[_from][msg.sender] -= _value;
emit Transfer(_from, _to, _value);
return true;
}
}
Explanation: This Solidity contract defines the $GCHAIN token adhering to the ERC-20 standard. It includes functionalities for transferring tokens, approving allowances, and transferring tokens on behalf of another address.
15. Solving the Blockchain Trilemma
15.1. Security
Golden Chain achieves robust security through its PoS mechanism, economic incentives, and cryptographic safeguards. The security parameter \( \lambda \) can be quantified as:
\[ \lambda = \frac{V}{C} \]
Where:
- \( V \) = Total value staked
- \( C \) = Cost to perform a 51% attack
A higher \( \lambda \) indicates stronger security.
15.2. Scalability
To address scalability, Golden Chain employs Layer 2 solutions and efficient block propagation protocols, achieving high transaction throughput without sacrificing decentralization or security.
\[ T = \sum_{s=1}^{S} T_s + T_{\text{Layer2}} \]
Where:
- \( S \) = Number of shards
- \( T_s \) = Transaction rate per shard
- \( T_{\text{Layer2}} \) = Transaction rate from Layer 2 solutions
15.3. Decentralization
Golden Chain promotes decentralization by maintaining a large and diverse set of validators. The decentralization index \( \Delta \) is calculated using the Gini Coefficient to measure inequality in stake distribution:
\[ \Delta = \frac{\sum_{i=1}^{N} \sum_{j=1}^{N} |S_i - S_j|}{2N^2 \mu} \]
Where:
- \( S_i \) = Staked tokens by validator \( i \)
- \( \mu \) = Mean staked tokens per validator
- \( N \) = Total number of validators
A lower \( \Delta \) indicates a more decentralized network.
15.4. Golden Chain's Solution
Golden Chain combines technological innovations and community-driven governance to address each aspect of the trilemma. By integrating efficient consensus mechanisms, scalable architecture, and decentralized governance, Golden Chain ensures a balanced and resilient blockchain platform.
| Trilemma Element | Golden Chain's Solution |
|---|---|
| Security | Enhanced PoS mechanism, slashing, and cryptographic protocols |
| Scalability | Sharding and Layer 2 integration |
| Decentralization | Diverse validator set and decentralized governance |
16. Comprehensive References
- Buterin, V. (2014). A Next-Generation Smart Contract and Decentralized Application Platform. Ethereum Whitepaper.
- King, S., & Nadal, S. (2012). PPCoin: Peer-to-Peer Crypto-Currency with Proof-of-Stake. PPCoin Whitepaper.
- Zheng, Z., Xie, S., Dai, H. N., Chen, X., & Wang, H. (2017). An Overview of Blockchain Technology: Architecture, Consensus, and Future Trends. 2017 IEEE International Congress on Big Data (BigData Congress).
- Gencer, A. E., Basu, S., Eyal, I., van Renesse, R., & Sirer, E. G. (2018). Decentralization in Bitcoin and Ethereum Networks. IEEE Symposium on Security and Privacy.
- Narayanan, A., Bonneau, J., Felten, E., Miller, A., & Goldfeder, S. (2016). Bitcoin and Cryptocurrency Technologies: A Comprehensive Introduction. Princeton University Press.
- Boneh, D., & Shoup, V. (2020). A Graduate Course in Applied Cryptography. Available at [https://crypto.stanford.edu/~dabo/cryptobook/](https://crypto.stanford.edu/~dabo/cryptobook/)
- Cachin, C., & Vukolić, M. (2017). Blockchain Consensus Protocols in the Wild. Proceedings of the 2017 ACM SIGSAC Conference on Computer and Communications Security.
- Kwon, J., & Min, K. (2020). Layer 2 Scaling Solutions for Blockchain Networks. IEEE Communications Surveys & Tutorials.
- Osterweil, E., & Buterin, V. (2021). Scalable Distributed Systems: Architectures and Protocols. MIT Press.
- Ben-Sasson, E., Chiesa, A., Genkin, D., Tromer, E., & Virza, M. (2014). Zerocash: Decentralized Anonymous Payments from Bitcoin. IEEE Symposium on Security and Privacy.
Additional references relevant to the advanced technical aspects and innovations of Golden Chain are included to provide a solid foundation for the whitepaper's assertions and methodologies.